Формула расчёта дисконтированного срока окупаемости

Положительные и отрицательные стороны данного показателя

Любой анализ показателей на предприятии несет в себе какой-либо экономический смысл и это очень важно, когда существует отдельный сотрудник, который может этим заниматься. Так, например, если возникает ситуация в поиске инвестора, для того, чтобы наладить обстановку в организации, очень наглядно будет представить ему расчет чистого дисконтированного дохода, который, во-первых продемонстрирует ситуацию на данный момент и в будущем, за счет вливания потоков средств инвестора и тогда будет ясно, стоит ли вкладывать средства в данное предприятие или лучше его закрыть и не погружаться в убытки и дальше

Так, например, если возникает ситуация в поиске инвестора, для того, чтобы наладить обстановку в организации, очень наглядно будет представить ему расчет чистого дисконтированного дохода, который, во-первых продемонстрирует ситуацию на данный момент и в будущем, за счет вливания потоков средств инвестора и тогда будет ясно, стоит ли вкладывать средства в данное предприятие или лучше его закрыть и не погружаться в убытки и дальше.

Плюсы	Минусы
Позволяет рассчитать практически все возможные риски связанные с вкладыванием средств в данный проект	Неточности расчетов, ведь невозможно все предусмотреть заранее точно, всегда есть доля погрешности
Инвестор наглядно видит всю картину, от ликвидности и рентабельности до убытков	Показатель инфляции так же влияет на расчет

Размер чистого дисконтированного дохода тесно взаимосвязан с таким инструментом анализа как ИПП (индекс прибыльности проекта). Этот параметр наглядно демонстрирует выгоду инвестора от участия в выбранном бизнесе. Для того чтобы определить величину ИПП, необходимо разделить совокупность дисконтированного дохода на размер запланированных трат.

Для этой цели используется формула: «ƩCFt/(1 + i)t/IC».

1. В том случае, когда значение ИПП превышает «0», инвестор окупит все вложенные средства.
2. Когда данный параметр имеет отрицательное значение, существует высокий риск потери имеющегося капитала.

Для того чтобы лучше понимать значение рассматриваемого параметра, следует рассмотреть практический пример. В качестве примера возьмем производственную компанию, которая внедряет на рынок новый ассортимент товаров (поэтапно на протяжении трех лет). Стоимость реализации данного проекта составляет два миллиона рублей на первом этапе (период при котором «t» равняется нулю). На следующих этапах, длительностью двенадцать месяцев, инвесторам необходимо затратить по одному миллиону рублей (t=1–3).

ЧДД= «-2/(1+0.1)0+(2-1)/(1+0.1)1+(2-1)/(1+0.1)2+(2-1)/(1+01.3)3=-2+0.9+0.83+0.75=0.48

По приведенным расчетам видим, что размер прибыли, составит 480 000рублей. Данный проект положителен и в него можно инвестировать средства, что выгодно инвесторам.

Значение ставки дисконтирования при расчёте NPV

Изучая чистую приведённую стоимость обязательно следует уделять серьёзное внимание показателю — ставка дисконтирования. Часто её именуют иначе — альтернативной стоимостью вложений

Показатель, используемый в формуле расчёта, обозначает минимальную величину доходности, которую инвестор считает для себя приемлемой при рисках, сопоставимых с имеющимися у реализуемого проекта.

Инвестор может оперировать средствами, привлекаемыми из различных источников (собственных либо заёмных).

1. В первом случае устанавливаемая ставка дисконтирования, является личной оценкой допустимых рисков рассматриваемого инвестиционного проекта.

Её оценка может иметь несколько подходов. Самые простые, это:

Выбор безрисковой ставки, корректируемой с учётом вероятности возникновения специфических рисков.

В качестве таковой обычно рассматриваются доходность по ценным бумагам государства, в котором реализуется проект, ставка доходности по корпоративным облигациям компаний отрасли.

Необходимая и минимально достаточная (с точки зрения потенциального инвестора) рентабельность (показатель ROE).

При этом, лицо, принимающее решение об инвестировании, определяет ставку дисконтирования по одному из возможных вариантов:

• в проект вкладываются средства, имеющиеся на депозите в конкретном банке. Следовательно, альтернативная стоимость не должна быть меньше имеющейся банковской ставки;
• В проект инвестируются средства, выведенные из бизнеса и являющиеся временно свободными. В случае возникновения потребности в них, оперативное изъятие всей суммы из проекта невозможно. Потребуется кредит. Поэтому в качестве текущей стоимости средств выбирается рыночная кредитная ставка;
• Средняя доходность основного бизнеса составляет Y%. Соответственно от инвестиционного проекта требуется получать не меньше.

2. При работе с заёмными средствами ставка будет рассчитана как величина производная от стоимости привлекаемых из различных источников средств.

Как правило ставка, устанавливаемая инвестором, в подобных случаях превышает аналогичный показатель стоимости заёмных денежных средств.

При этом не просто учитывается изменение стоимости средств во времени, но и закладываются возможные риски, связанные с неопределённостью поступления денежных потоков и их объёмов.

Это является главной причиной, по которой ставкой дисконтирования считают средневзвешенную стоимость привлекаемого для последующего инвестирования капитала (WACC).

Именно этот показатель рассматривается в качестве требуемой нормы доходности на средства, вложенные в конкретный инвестиционный проект.

Чем выше ожидаемые риски, тем выше ставка.

Расчётные методы определения данного параметра менее наглядны, чем графические. Особенно когда требуется сравнить привлекательность двух или более проектов.

Например, сравнивая проекты «А» и «Б» (смотри график) можно сделать следующие выводы:

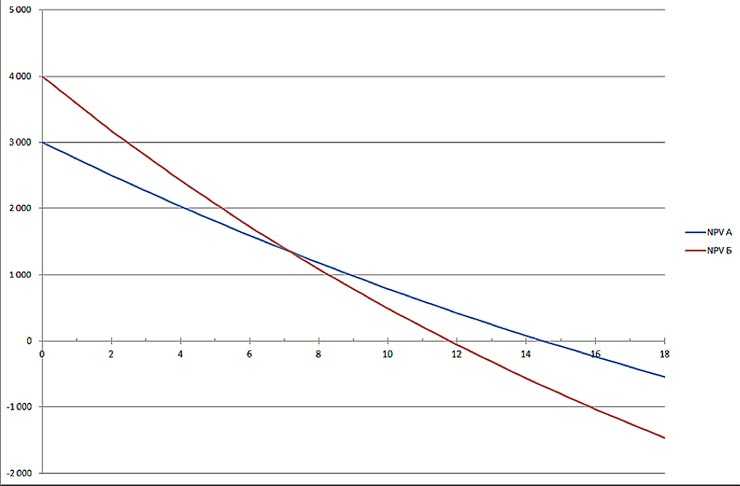
При ставке, превышающей значение 7%, величина NPV проекта А выше, чем у Б (что предупреждает о возможной ошибке в выборе при арифметическом сопоставлении).

К тому же инвестиционный проект «Б», обозначенный на графике красной кривой, подвержен более значительным изменениям в связи с изменяющейся ставкой дисконтирования (такое может быть объяснено разновеликими величинами поступающих средств в одинаковый период времени).

Следует учитывать факт существенного снижения величины ставок дисконтирования во времени, что накладывает определённые временные ограничение. Рассчитать их можно не более, чем за 10 лет.

Анализ графиков позволяет сделать вывод о том, что меняющаяся ставка дисконтирования приводит к изменениям величины показателя NPV (причём последний меняется нелинейно).

Поэтому для более взвешенной оценки необходимо не просто сравнивать величины для разных инвестиционных проектов, но и учитывать изменения последних при разных величинах ставки.

По умолчанию при расчете в Excel, ставка дисконтирования принимается равной 10%.

Чистая текущая стоимость проекта (Net present value, NPV)

Данный показатель определяют как разность между текущей стоимостью денежных поступлений по проекту или инвестиций и текущей стоимостью денежных выплат на получение инвестиций, либо на финансирование проекта, рассчитанная по фиксированной ставке дисконтирования. Значение NPV можно представить как результат, получаемый немедленно после принятия решения об осуществлении данного проекта, так как при расчете NPV исключается воздействие фактора времени, то есть если значение показателя:

• NPV > 0 – проект принесет прибыль инвесторам;
• NPV = 0 – увеличение объемов производства не повлияет на получение прибыли инвесторами;
• NPV < 0 – проект принесет убытки инвесторам.

Первая особенность чистой текущей стоимости проекта (чистого приведенного дохода) состоит в том, что, являясь абсолютным показателем эффективности инвестиционного проекта, он непосредственно зависит от его размера. Чем большим является размер инвестиционных затрат по проекту и соответственно сумма планируемого чистого денежного потока по нему, тем более высоким (при прочих равных условиях) будет абсолютная сумма NPV.

Вторая особенность чистой текущей стоимости проекта заключается в том, что на ее сумму сильное влияние оказывает структура распределения совокупного объема инвестиционных издержек по отдельным периодам времени проектного цикла. Чем большая доля таких затрат осуществляется в будущих периодах проектного цикла (по отношению к его началу), тем большей при прочих равных условиях будет и сумма планируемого чистого приведенного дохода по нему. Наименьшее значение этого показателя формируется при условии полного осуществления инвестиционных затрат с наличием проектного цикла.

Третья особенность чистой текущей стоимости проекта состоит в том, что на его численное значение существенное влияние оказывает время начала эксплуатационной стадии (по отношению к времени начала проектного цикла), позволяющее начать формирование чистого денежного потока по инвестиционному проекту. Чем продолжительней временной интервал между началом проектного цикла и началом эксплуатационной стадии, тем меньшим при прочих равных условиях будет размер NPV.

И наконец, особенность чистого приведенного дохода заключается в том, что его численное значение сильно колеблется в зависимости от уровня дисконтной ставки приведения к настоящей стоимости основных показателей инвестиционного проекта – объема инвестиционных затрат и суммы чистого денежного потока.

На величину NPV влияют два вида факторов: производственный процесс (больше продукции – больше выручки, меньше затраты – больше прибыли и т.д.) и ставка дисконтирования. А также оказывает влияние масштаб деятельности, выраженный в «физических» объемах инвестиций, производства или продаж.

Отсюда вытекает естественное ограничение на применение данного метода для сопоставления различных по этой характеристике проектов: большее значение NPV не всегда будет соответствовать более эффективному варианту капиталовложений. В подобных случаях рекомендуется использовать показатель рентабельности инвестиций, называемый также коэффициентом чистой текущей стоимости (NPVR).

Указанный показатель представляет собой отношение чистой текущей стоимости проекта к дисконтированной (текущей) стоимости инвестиционных затрат (РVI).

Тщательный анализ результата

Специалистами было разработана базовое правило, обязательное для оценки уровня КПД инвестиций — принять план-проект можно только в том случае, если итоговая величина имеет значение «+». Если же этот параметр «-», то рассматриваемый инвестиционный проект будет убыточным. Цифра «0» свидетельствует о том, что доходные потоки от реализуемой программы могут возместить затратную часть, без поступления прибыли.

Такой подход позволяет узнать следующие данные: плотность, размещение средств, возвратность и единовременное погашение:

• PV — это общая сумма финсредств для размещения на общих условиях срочности, плотности и возвратности.
• FV — сумма, которая может быть использована для погашения долга. Включает в себя размер займа, проценты.
• r — процентная ставка, используемая в качестве платы за те финансы, которые были взяты в кредит.

Вычисление приведенной стоимости

В примере, приведенном ниже в этом разделе, вычисляется приведенное значение серии будущих выплат, иногда называемых ежегодной рентой. Если каждый год в течение десяти лет вносится платеж размером в 1200 долларов, то приведенная стоимость этих платежей составляет 6780,27 долларов: . Другими словами, если плательщик в настоящий момент предложит вам 6800 долларов, вам будет выгоднее их взять, чем получать в течение 10 лет по 1200 долларов. Если он предложит меньшую сумму, лучше подождать регулярных ежегодных платежей.

В приведенной выше формуле вы, наверное, заметили, что процентная ставка взята как бы ниоткуда. Функция ПС обычно используется для определения, сколько стоят на настоящий момент будущие выплаты. В этих ситуациях конкретная процентная ставка недоступна.

Существует множество мнений относительно того, какую процентную ставку лучше использовать при определении приведенной стоимости. Выбор процентной ставки в значительной мере зависит от вас самих. Одни говорят, что нужно использовать текущую процентную ставку по банковским депозитам, другие утверждают, что нужно брать процентную ставку по инвестициям, не связанным с рисками, таким как казначейские облигации. В данном примере была использована процентная ставка по инвестициям в ценные бумаги.

В приведенном выше примере была использована процентная ставка 12%. В результате получилось, что инвестиция размером в 6800 долларов принесет тот же доход, что и десятилетнее ожидание платежей по 1 200 долларов. Если плательщик предложит вам 7000 долларов немедленно, вы можете вложить их и получить лучший финансовый результат. Теперь давайте вернемся к таблицам и предположим, что у вас есть обязательства, по которым вы должны ежегодно выплачивать кому-то по 1200 долларов в течение 10 лет. Формула выглядит следующим образом: .

Вместо входящего, в этой формуле использован исходящий денежный поток. Результат (-$6 780,27) также имеет знак, противоположный предыдущему примеру. В обоих примерах сумма платежей формирует всю транзакцию, поэтому будущей стоимости не существует. Также в примере использовано значение по умолчанию аргумента Тип. Аргументы БС и Тип не являются обязательными; они были включены в пример только для наглядности. На рис. 1 этот расчет показан в рабочей книге.

Рис. 1. Вычисление приведенной стоимости

Из соображений простоты в формулах примеров, приведенных в тексте, используются только константы. На практике чаще всего в аргументы функций подставляются ссылки на ячейки.

Приведенная стоимость единовременной будущей выплаты

В предыдущих примерах мы имели дело с сериями последовательных регулярных выплат, однако иногда существует всего одна будущая единовременная выплата. В качестве примера представим себе, что некоторый богатый родственник решил дать вам 100 тысяч долларов, но вы не можете получить их до своего сорокалетия. Если сейчас вам 25 лет, приведенная стоимость будущего платежа составит 31524,17 долларов. Эта сумма получена с помощью следующей формулы: .

Таким образом, это будет единовременный платеж ровно через 15 лет. Если бы у вас были сейчас какие-либо деньги, вы смогли бы инвестировать их под 8% годовых. Так как периодических платежей не будет, аргумент Тип в формуле опущен. Результат формулы свидетельствует о том, что если бы у вас было сейчас 31524,17 долларов и вы бы инвестировали их под 8%, то через 15 лет получили бы сотню тысяч долларов.

Рис. 2. Приведенное значение будущей единовременной выплаты

Особенности ключевых критериев эффективности проекта

Поскольку оба метода чрезвычайно популярны в среде экономистов и финансистов, то стоит изучить подробнее, какой из них способен дать более объективную информацию. Сравнительная характеристика критериев NPV и IRR показывает, что у каждого из этих финансовых инструментов есть свои сильные и слабые стороны.

Отличительными чертами NPV являются:

• Прямая зависимость показателя от масштаба бизнеса: чем крупнее инвестиции и больше объем денежного потока, тем выше будет значение показателя текущей стоимости.
• Влияние на значение критерия структуры финансирования по временным отрезкам.  Если проект проходит через все этапы затрат (проект, начальные вложения, затраты на ликвидацию), то его величина, скорее всего, будет минимальна.
• Влияние длительности временного лага между инвестированием и сроками начала эксплуатации объекта, чем больше перерыв, тем меньше величина NPV. Кроме того, динамика барьерной ставки может сильно повлиять на дисконтируемую сумму инвестиций.

На численное значение показателя основное влияние оказывают такие факторы:

• Норма дисконта.
• Темпы процесса производства: меньше затраты – больше прибыль – больше объем выручки.
• Масштаб компании, зависимость от количества выпущенной продукции, объемов продаж, суммы вложения.

К достоинствам внутренней нормы прибыльности можно отнести:

• Возможность провести сравнение между проектами, которые имеют различную длительность, темпы производства и масштабы инвестирования.
• Возможность оценивания не только инвестиционных проектов, но и других альтернативных финансовых инструментов (например, вклад на банковский депозит). Если IRR инвестиционного начинания окажется выше процентной ставки по депозиту, то более выгодно инвестировать в проект.
• Быстрое определение целесообразности дальнейшего анализа предложенного проекта после его экспресс-оценки на норму внутренней доходности. При этом производится оценка IRR относительно WACC (стоимости капитала средневзвешенной). Если IRR больше WACC, то начинание обещает прибыль, если же меньше или значения равны, то следует ожидать отрицательного потока денег в будущем.
• Показатель IRR может применяться в качестве ставки дисконтирования. Чем больше разница между внутренней нормой доходности и нормативной рентабельностью, тем более интересно инвестиционное предложение.

Однако есть у критерия внутренней нормы прибыльности и свои недостатки, среди них:

• Невозможность показать рост стоимости проекта в абсолютных величинах.
• Трудность расчета и возможность получения некорректного результата при несистематической структуре денежных потоков (с попеременным отрицательным и положительным значением).

Финансисты в паре NPV – IRR предпочитают больше применять второй метод, поскольку для него нет необходимости высчитывать ставку дисконтирования, как для чистой приведенной стоимости. Кроме того, результат при определении нормы прибыльности внутренней рассчитывается в процентах, поэтому им удобнее пользоваться при сравнении относительных величин (процентов), а чистая дисконтированная стоимость исчисляется в денежных знаках, соответственно, меньше приспособлена для сравнения. Хотя большинство учебников утверждает, что NPV указывает на величину создаваемой инициативой добавленной стоимости, поэтому должно быть предпочтительнее.

Нередко указанные выше ключевые показатели дают результаты, противоречащие друг другу. Причиной этого может быть заложенная в расчет ставка дисконта или нестандартная структура финансовых потоков. При этом NPV характеризует размер будущего дохода, а IRR – темпы его получения. На каком варианте лучше остановиться? Специалисты по финансовому анализу рекомендуют в таком случае выбирать критерий текущей стоимости, поскольку в нем учитывается переменная норма дисконта, а главной целью вложения является объем прибыли, а не скорость ее получения.

Как можно видеть из сказанного, IRR и NPV являются ключевыми показателями эффективности инвестиционного предложения. Взяв их за основу, инвестор или владелец бизнеса может просчитывать и другие вспомогательные показатели, такие как индекс доходности (PI), дисконтированный срок окупаемости (DPP), средневзвешенная ставка инвестиционной рентабельности (ARR).

Преимущества и недостатки

Преимущества:

1. Учитывается относительная стоимость денег. Иными словами, реальное отражение цифр, а не красивые описания.

2. Можно соотносить с разной степенью риска, увеличивая или уменьшая ставку дисконтирования. Выше процент — выше риск, ниже процент — ниже риск.

3. Возможность сравнивать схожие проекты. Так как денежные потоки «нормируются» по отношению к исходной точке в виде единого параметра, то их становится существенно проще сравнивать, чем огромные отличающиеся друг от друга наборы чисел.

4. Четкие критерии оценки. Например, рассматривать или не рассматривать проекты, ЧДД которых по фиксированной ставке дисконтирования больше или меньше нуля.

Недостатки:

1. Расчет ставки дисконтирования не так прост (неоднозначная природа самого процента). Например, если проект подразумевает несколько разных частей (или состоит из нескольких), то какой должен быть процент для всего потока денег? Допустим, проект состоит из нескольких малорисковых и нескольких высокорисковых. Как вычислять процент? Среднее? Отклонение? Или иной математический подход?

2. Не учитывается вероятность каждого денежного потока. Денежные потоки рассчитываются относительно их исторических значений или вообще являются чистым предположением (например, если товара ранее не существовало). Поэтому, чистый дисконтированный доход это оценка одного конкретного варианта. 

3. Формула чувствительна к составляющим. Например, если периоды у проектов отличаются, то их уже некорректно сравнивать (как минимум, денежные потоки нелинейны)

Или если, например, отличаются суммы вложений, то это так же может быть нетривиальным (чем больше сумма, тем выше риск и больше важности у процента)

4. Сложно сравнивать диапазоны. Каждый последующий поток в меньшей степени влияет на значение NPV. Например, +100 или -100 в первом периоде это +82,64 или -82,64, а вот в 5-м это +62,09 и -62,09.

Стоит отметить, что для минимизации недостатков применяют расширенные подходы. Например, вычисляют индекс скорости удельного прироста стоимости.

Применение приведённой NPV на практике

Универсальные формулы приведённой стоимости активно используют опытные и начинающие инвесторы. Такой подход помогает оценить целесообразность внесения финсредств. Эксперты рекомендуют использовать три варианта расчёта приведённой NPV:

1. Если чистая стоимость в приведённый период =0, это указание, что инвестиции окупаются, но сам вкладчик не получит никакой прибыли. К примеру: если гражданин использовал кредитные деньги, то поступающие финпотоки благоприятствуют расчёту с кредитором полностью. Инвестор сможет выплатить все начисленные %, а сам счёт останется неизменным. Здесь лучше найти иные варианты вклада, с более оптимистичным приведённым результатом чистой итоговой стоимости.
2. Когда при изучении приведённого показателя NPV было получено плюсовое значение стоимости, то инвестиция полностью окупается. А сама цифра отображает цифру прибыли вкладчика. Конечно, в этом случае инвестиции более чем оправданы, так как в итоге человек получает хорошую прибыль.
3. В редких случаях после многочисленных расчётов стоимости выходит отрицательное значение приведённой цифры. В такой ситуации инвестиции пользователя не окупаются, а сам вкладчик остаётся с убытками. Если исследуемый проект с минусовым значением, от работы с ним правильнее отказаться.

Дисконтирование и компаундирование

Когда речь идёт о том,
чтобы соотнести все будущие денежные
потоки относительно настоящего момента
времени, то речь идёт о дисконтировании.
В тех же случаях когда, наоборот, денежные
потоки приводятся к определённой точке
в обозримом будущем — речь идёт уже о
компаундировании (или наращении) денежных
потоков.

Для простоты понимания
вот вам два примера.

Пример первый.
Дисконтирование

Допустим вы поставили
себе целью поездку на очередные
Олимпийские игры которые должны
состояться ровно через 4 года. Вы
подсчитали, что с учётом всех сопутствующих
расходов (билеты, проезд, проживание и
т.п.) вам потребуется сумма денег в 10000
долларов.

Сумма эта достаточно
серьёзная для того, чтобы просто взять
и вырвать её из своего семейного бюджета,
поэтому вы решаете позаботиться о её
накоплении заранее. Можно начать
ежемесячно откладывать деньги. А можно
рассчитать какую сумму денег необходимо
вложить в банк сейчас, чтобы через 4 года
размер вклада достиг требуемых 10000
долларов.

Допустим вы решили
вложить деньги в банк под 7% годовых.
Рассчитать требуемую сумму вклада при
этом можно умножив требуемые 10000$
на коэффициент дисконтирования
вычисляемый по формуле:

Подставляя в формулу
наши цифры и умножая на 10000 получим:

10000*(1/(1+0,07)^4))=7633,58$

То есть, для того чтобы
через четыре года получить требуемые
10000$ вам потребуется
вложить в банк 7635$.

Приведённый выше расчёт есть ни что иное как дисконтирование

Обратите внимание, что при его проведении мы двигались от денежных сумм в будущем к суммам в настоящем. Или, оперируя общепринятыми терминами, от будущей стоимости FV (Future Value) к стоимости текущей PV (Present Value)

Пример второй.
Компаундирование

Теперь рассмотрим
другой пример. Допустим у вас образовался
определённый излишек денежных средств,
которые вам вряд ли потребуются в
ближайшие пять лет и вы хотите их
приумножить ничем при этом практически
не рискуя. Самый безрисковый вариант в
данном случае опять же банковский
депозит.

Пускай у вас есть
средства в размере 5000$ которые
вы готовы вложить под 7% годовых на срок
в 5 лет. Прибыль от этого вклада можно
рассчитать умножив вкладываемую сумму
денег на коэффициент наращения вычисляемый
по формуле:

Подставим наши цифры,
умножим на 5000 и получим:

5000*(1+0,07)^5=7012,75$

То есть, в итоге
через пять лет сумма вклада вырастет
до 7012 долларов. В данном примере мы
рассмотрели с вами операцию наращения
или компаундирования в которой опять-таки
фигурировали две основные составляющие
в виде текущей и будущей стоимости:

• PV=5000 долларов;
• FV=7012,75
  долларов.

Обратите внимание на
то, что проводя данный расчёт мы с вами
двигались от денежных сумм в настоящем,
к суммам в будущем времени

Пример анализа ЧПС

Предприятие оценивает два проекта. В первый необходимо вложить 1,2 млн. рублей, а во второй – 1,4 млн. рублей. Согласно плану, денежные потоки от будущего бизнеса составят:

• 2022 год: 0,3 млн. руб. по первому проекту, 0,35 млн. руб. – по второму;
• 2023 год: 0,41 млн. руб. – первый; 0,51 – второй;
• 2024 год: 0,5 млн. руб. – первый; 0,6 млн. руб. – второй;
• 2025 год: 0,65 млн. руб. – первый, 0,63 млн. руб. – второй.

Компании нужно оценить ЧПС за 4 года и проанализировать показатели. На основании итогов исследования будет сделан выбор в пользу того или иного варианта. Известно, что ставка дисконтирования равна 25%.

Пример расчета ЧПС первого проекта

Исследуемый период равен 4 годам. В качестве денежного потока за каждый промежуток времени принимаются плановые показатели. Теперь необходимо их переоценить с применением коэффициента дисконтирования. Для его определения используем сокращенную формулу ЧПС:

 (1 + РСД) Т,

где Т – период, за который рассчитывается показатель;

РСД – ставка дисконтирования.

Так как ставка дисконтирования указана в процентах, ее необходимо перевести в десятичное число: 25 / 100 = 0,25.

(1 + 0,25)4 = 2,44 – коэффициент дисконтирования.

Далее достаточно перемножить денежные потоки по годам с коэффициентом дисконтирования:

• 2022 год: 0,3 млн. руб. / 2,44 = 0,123 млн. руб.;
• 2023 год: 0,41 млн. руб. / 2,44 = 0,168 млн. руб.;
• 2024 год: 0,5 млн. руб. / 2,44 = 0,205 млн. руб.;
• 2025 год: 0,65 млн. руб. / 2,44 = 0,266 млн. руб.

Теперь можно найти ЧПС:

0,123 млн. руб. + 0,168 млн. руб. + 0,205 млн. руб. + 0,266 млн. руб. = 0,762 млн. руб.

Чтобы понять, покроют ли будущие денежные притоки вложения, из суммы инвестиций отнимем рассчитанное выше значение:

1,2 млн. руб. – 0,762 млн. руб. = 0,438 – положительное значение показывает, что доходность от реализации проекта не покроет расходы в полном объеме.

Можно пойти более легким путем и рассчитать показатель путем подстановки данных в общую формулу:

1,2 – (0,3 + 0,41 + 0,5 + 0,65) * (1 + 0,25)4 = 0,438

Пример расчета ЧПС второго проекта

Ранее мы уже рассчитали коэффициент дисконтирования и определили временной промежуток, равный 4 годам. Теперь нужно переоценить финансовые потоки второго проекта:

• 2022 год: 0,35 млн. руб. / 2,44 = 0,143 млн. руб.;
• 2023 год: 0,51 млн. руб. / 2,44 = 0,21 млн. руб.;
• 2024 год: 0,6 млн. руб. / 2,44 = 0,245 млн. руб.;
• 2025 год: 0,63 млн. руб. / 2,44 = 0,258 млн. руб.

Теперь можно найти ЧПС путем сложения переоцененных денежных потоков:

0,143 млн. руб. + 0,21 млн. руб. + 0,245 млн. руб. + 0,258 млн. руб. = 0,856 млн. рублей.

Сравним доходность с вложениями:

1,4 млн. руб. – 0,856 млн. руб. =  0,544 млн. руб.

Анализ ЧПС двух проектов

Расчет ЧПС показал, что по первому проекту показатель будет равен 0,438 млн. руб., а по второму – 0,544 млн. руб. Получается, что обе программы не окупят вложения в полном объеме. Однако по первому проекту остаток непогашенных вложений гораздо меньше, чем по второму. Поэтому компания будет инвестировать средства в развитие первой программы.

Важные нюансы

Математически рассчитать ЧДД несложно. При условии, что Вам точно известны все переменные для расчета текущей стоимости инвестиционного проекта. Но как раз здесь и начинаются сложности…

Как определить ставку дисконтирования R?

Как правило, ставка дисконтирования – это процент, под который инвестор может привлечь финансовые ресурсы. И таких способов достаточно много:

• Банковский кредит.
• Займ у знакомых под минимальный процент.
• Продажа активов, вывод денег из других проектов или личные накопления.

Во всех этих вариантах стоимость капитала будет разной! Даже ставка по кредиту будет варьироваться в зависимости от финансовой устойчивости компании, сроков, суммы и наличия обеспечения.

Как найти ставку дисконтирования? Чаще всего инвесторы рассчитывают средневзвешенную величину процентных ставок всех потенциальных источников.

Такой способ расчета дисконта по капиталу называется WACC (сокращение от Weighted Average Cost of Capital).

Как определить размер денежных потоков (CF)?

Пожалуй, это самый сложный этап. Нам нужно заранее знать суммы всех поступлений по проекту и затрат на него. Если это касается бизнеса или компании инвестора, то придется рассчитывать объемы и суммы будущих продаж, а также сделать точную калькуляцию всей затратной части (аренда, сырье, налоги, зарплата, логистика и т.д.).

Как интерпретировать полученный результат?

Если NPV > 0, то проект принесет прибыль

Если NPV< 0, то вариант убыточен. Нужно либо отказаться от него, либо пересмотреть исходные данные.

Если NPV = 0, то проект полностью окупит вложенные в него средства, но прибыли инвестору не принесет.

Простые примеры расчета и практическое применение

Пример 1

Оцениваем ЧДД проекта «Кофейня». Ставку дисконтирования принимаем на уровне 10%.

Статья	1 год	2 год	3 год	4 год	5 год
Инвестиции в проект	100 000
Операционные доходы		25 000	27 000	34 000	40 000
Операционные расходы		8 000	7 000	6 000	4 000
Чистый денежный  поток	-100 000	17 000	20 000	28 000	36 000

Считаем NPV по формуле в Excel, не забыв отдельно вписать в нее первоначальные инвестиции со знаком «-».

NPV получилось отрицательным (-22 391 рубля). При таких исходных данных проект «Кофейня» за пять лет не выйдет даже в ноль. Но не исключено, что через определенный момент времени бизнес может стать прибыльным.

Пример 2

Появилась возможность выгодно купить недвижимость в Болгарии под сдачу в аренду за символические $40 000. Знакомый согласился одолжить эту сумму на 5 лет под 9% годовых (ставка дисконтирования равна 0,09).

Предполагаемый доход от сдачи в аренду за год: от $13 000 до $19 000 (расчеты делала управляющая компания).

Анализ проекта с помощью NPV выглядит так.

Статья	1 год	2 год	3 год	4 год	5 год
Инвестиции в проект	40 000
Чистый денежный поток	-40 000	13 000	15 000	17 000	19 000

Подставляя значения формулу в Excel, получаем дисконтированный доход NPV = $11 139.

Индекс прибыльности инвестиций (Profitability index, PI)

Показатель иллюстрирует отношение отдачи капитала к размеру вложенного капитала, показатель прибыльности инвестиций показывает относительную прибыльность проекта или дисконтируемую стоимость денежных поступлений от проекта в расчете на единицу вложений. Индекс прибыльности рассчитывается по формуле:

PI = NPV / I, где I — вложения.

Рассматривая показатель «индекс (коэффициент) доходности», необходимо принять во внимание то, что данный ппоказатель является относительным, описывающим не абсолютный размер чистого денежного потока, а его уровень по отношению к инвестиционных затратам. Это преимущество индекса прибыльности инвестиций позволяет использовать его в процессе сравнительной оценки эффективности инвестиционных проектов, различающихся по своим размерам (объему инвестиционных затрат)

Кроме того, PI может быть использован и для исключения неэффективных инвестиционных проектов на предварительной стадии их рассмотрения. Если значение индекса (коэффициента) доходности меньше единицы или равно ей, инвестиционный проект должен быть отвергнут в связи с тем, что он не принесет дополнительный доход на инвестируемый капитал (не обеспечит самовозрастания его стоимости в процессе инвестиционной деятельности).

Критерий принятия решения такой же, как при принятии решения по показателю NPV, т.е. РI > 0. При этом возможны три варианта:

• РI > 1,0 – инвестиции рентабельны и приемлемы в соответствии с выбранной ставкой дисконтирования;
• РI < 1,0 – инвестиции не способны генерировать требуемую ставку отдачи и неприемлемы;
• РI = 1,0 – рассматриваемое направление инвестиций в точности удовлетворяет выбранной ставке отдачи, которая равна IRR.

Проекты с высокими значениями PI более устойчивы. Однако не следует забывать, что очень большие значения индекса (коэффициента) доходности не всегда соответствуют высокому значению чистой текущей стоимости проекта и наоборот. Дело в том, что проекты, имеющие высокую чистую текущую стоимость не обязательно эффективны, а значит, имеют весьма небольшой индекс прибыльности.

Рассмотрим, какими свойствами обладает показатель PI.

Благодаря этому критерий PI очень удобен при выборе одного проекта из ряда альтернативных, имеющих примерно одинаковые значения NPV, но разные объемы требуемых вложений. Из этих проектов выгоднее тот, который обеспечит их большую эффективность.

1. Индекс рентабельности является относительным показателем. Он характеризует уровень доходов на единицу затрат, т.е. эффективность вложений – чем больше величина PI, тем выше отдача от каждого рубля, инвестированного в проект.

2. Показатель позволяет ранжировать различные инновационные проекты с точки зрения их привлекательности. Критерий оптимальности при сравнении проектов, имеющих примерно равные значения чистого приведенного дохода: PI → max.

3. Применение показателя часто бывает полезным, когда существует возможность финансирования нескольких проектов, но инвестиционный бюджет ограничен. Этот показатель косвенно несет в себе информацию о риске проекта, т.е. о его устойчивости к изменению исходных параметров.